"2D Fokker-Planck models of rotating clusters"

back to main (back to main)

1. Theory

We use the method developed by Goodman (1983) based on the solution of an orbit-averaged 2D Fokker-Planck equation, written in terms of E, Jz (isolating integrals of moltion in a general axisymmetric potential):

Where

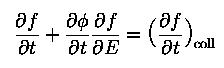
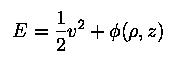  and   

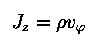
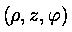(cylindrical coordinates were used)

The initial models are rotating King models of the form

Where:

E: energy of the system,  Jz: angular momentum,  Ω0: central rotational velocity
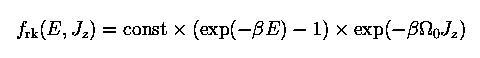
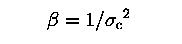,  σc: central velocity dispersion

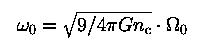Initial conditions are determined by:

,dimensionless angular velocity (rotating parameter)
G=1, nc: central density

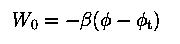,dimensionless potential (King parameter)
Φt: tidal potential

The age of the system is given in units of the initial half mass relaxation time:


rh is the half mass radius and M the total cluster mass. The dynamical time scale t0 is defined in  Cohn (1979) .

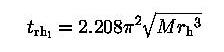
The dynamical ellipticity is calculated following Goodman (1983), given by


Where s ≡ b/a = 1 - edyn, Trot is the rotational energy, TσΦ is the energy contained in the azimuthal component of the velocity dispersion and Tσ represents the energy of all components of the velocity dispersion.

back to main (back to main)

2. Model classification

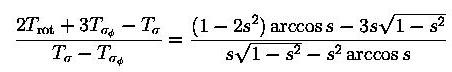
Initial parameters of the 12 rotating cluster models.

TABLE 1
King parameter Worotating parameter ωo
3.00.00.300.600.90
6.00.00.300.600.90
9.00.00.060.080.10


back to main (back to main)

3. Time-Ellipticity Grid

Evolution grid in interval coordinates for the 12 models. The cells contain the total number of datasets available for the grid point with given time and ellipticity.

TABLE 2
EllipticityTime (t/trh)
(0,2)(2,4)(4,6)(6,8)(8,10)(10,12)
(0.00-0.02)591640935858
(0.02-0.04) 5241510 
(0.04-0.06)827914  
(0.06-0.10)2862112  
(0.10-0.15)19243   
(0.15-0.20)67    
(0.20-0.25)4     
(0.25-0.30)5     
(0.30-0.50)3     


back to main (back to main)

4. Time evolution of main parameters

We present the evolution in time of global parameters, classified by initial King- and rotating parameters (see description below)

TABLE 3
Model (Wo, ωo)Datafiles
(3,0.00)time030_000
(3,0.30)time030_030
(3,0.60)time030_060
(3,0.90)time030_090
(6,0.00)time060_000
(6,0.30)time060_030
(6,0.60)time060_060
(6,0.90)time060_090
(9,0.00)time090_000
(9,0.06)time090_006
(9,0.08)time090_008
(9,0.10)time090_010


Description of data:
Column 1: Time(t/t_rh) THTIO
Column 2: Timestep NSTEP
Column 3: Time (t/t_rc) TCTIO
Column 4: Core radius RCORE
Column 5: Central density XRHO(1,1)
Column 6: Central rotational velocity VROT(1,1)
Column 7: Central 1-dim Velocity dispersion XSIGT(1,1)
Column 8: Ellipticity EDYN
Column 9: Escape energy SEE
Column 10: Collapse rate XI
Column 11: Total mass XMTOT
Column 12: Total ang. momentum XJTOT
Column 13: Total potential energy XPTOT
Column 14: Total kinetic energy XKTOT

back to main (back to main)

5. Plot samples

Some examples of what kind of plots can be produced with the datasets

5.1. Evolution of the central density



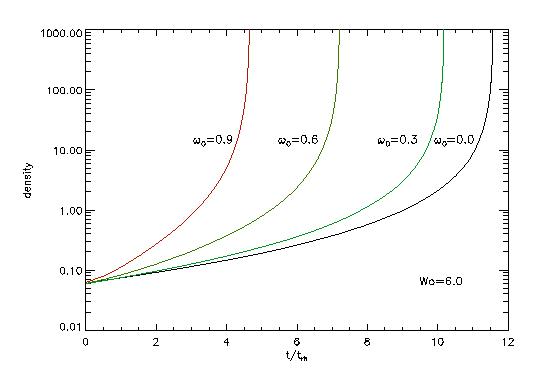
The figure shows the acceleration of core-collapse due to rotation (central density in code units vs. time). The black line represents a non-rotating, the red line a high initial rotating case (ωo=0.9). See also Fig. 3 of Fiestas et al. 2004.

idl logo -routine to generate the plot: dtime.pro

5.2. Distribution function


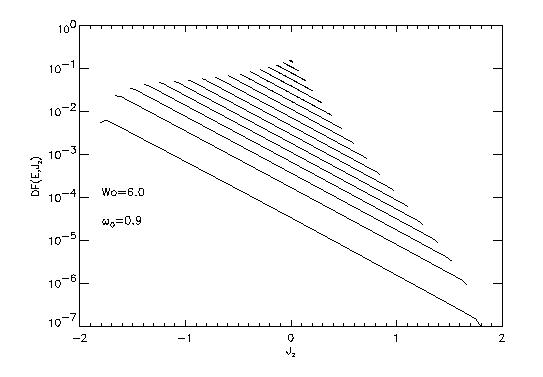
The figure shows the initial distribution function (King model) against angular momentum (curves of constant energy) for the model (6.0,0.3) See also Figs. 1 and 2 of Fiestas et al. 2004.

idl logo -routine to generate the plot: df.pro

5.3. Rotational velocity


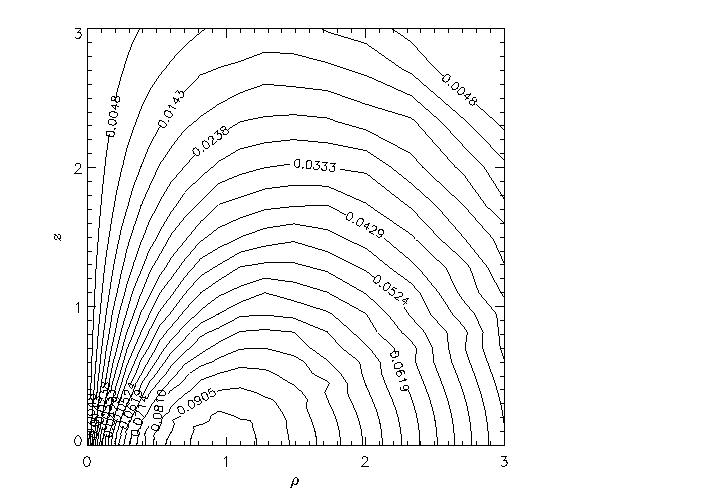
The figure shows a contour map (on meridional plane) of the rotational velocity for a collapsed model of initial (6.0,0.9) at time t/trh=4.7. Distances are given in units of initial core radius, velocity in code units.

idl logo -routine to generate the plot: vrot.pro

5.4. Velocity dispersion


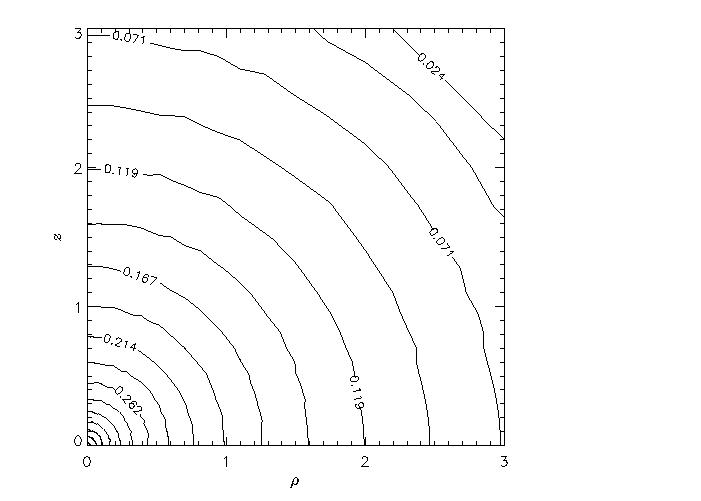
Contour map of 1-d velocity dispersion (on meridional plane) for a collapsed model of initial (6.0,0.9) at time t/trh=4.7. Distances are given in units of initial core radius, velocity in code units.

idl logo -routine to generate the plot: vdisp.pro

4.5. Ellipticity

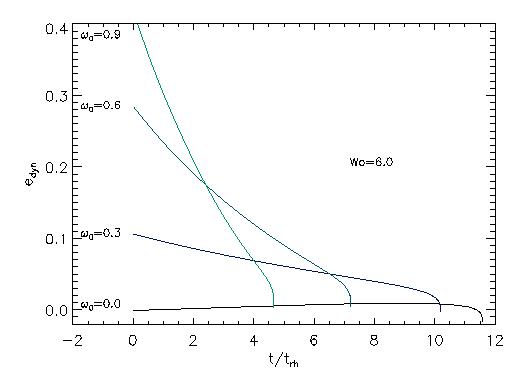
Download

This figure shows the time evolution of dynamical ellipticity for the model Wo=6 and different initial rotation parameters (See also Fig. 4 of Fiestas et al. 2004).

idl logo -routine to generate the plot: edynage.pro

back to main (back to main)

References:
  1. Cohn (1980), Astrophys. J. 242, p765.
  2. Einsel C.. & Spurzem R. (1999), MNRAS, 302, p81. Paper I
  3. Gebhardt K., Pryor C., O'Connell R.D., Williams T.B.,Hesser J.E. (2000), Astrophys. J. 119, p1268
  4. Goodman (1983), PhD Thesis, Princeton University
  5. Kim E., EInsel C., Lee H.M., Spurzem R., Lee M.G. (2002),MNRAS 334, p310.Paper II
  6. King I.R., Anderson J. (2001), in S. Deiters et al., (eds), Dynamics of Star Clusters and the Milky Way, ASP Conf. Ser. 228, p19
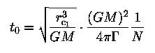t0 is defined in Cohn (1979) as and set to 1